With the recent pandemic disease caused by covid-19 virus, it is important to develop models that can better monitor how the disease will be propagated with time. We can check the total Covid cases that have occurred across the world from Jan 2020 till present day. This will provide a nice summary of the evolution of disease spread across time.
In this post, we would be going through some basic compartmental-based models which could be helpful is understanding the underlying mechanism of the disease spread in time. This could be a motivation to create certain hybrid set of models that combined the benefits of these maths-based models with data-driven models.
- Some preliminary definitions
- Infectious Disease Modeling
- Compartmental Models
- Interventions
- Treatment or Vaccination
- How to counter the spread of disease?
- Useful Resources
Some preliminary definitions
Some of the common used terms used while developing mathematical models for infectious disease modeling are given as below:
-
Prevalence of infection – It is defined as the total number of infected people at a given point in time.
-
Incidence of infection – It indicates the total number of new cases in a given interval of time (say per day, per week).
-
Incubation period – It is defined as a period between exposure and onset of symptoms.
-
Latent period – It is defined as a period immediately following exposure when the individual is infected but not infectious.
-
Infection term, \( \beta \) – It is defined as the average number of secondary infections per unit time.
-
Force of Infection, \( \lambda \) – It is a force that is acting on susceptible people in the population and is working to turn them into infected people.
-
Recovery rate, \( \gamma\) – It is defined as the hazard rate of recovery from infection.
-
Mortality rate, \( \mu \) – It is the rate at which death of individuals occurs, per unit time.
-
Case fatality rate – It is the proportion of the people who die as as result of the disease. It is described as: \[\text{Case fatality rate } = \frac{\mu}{\mu + \gamma} \]
-
Survival rate – It is the proportion of the people who recover and survive. It is described as: \[\text{Survival rate } = \frac{\gamma}{\mu + \gamma} \]
-
Reproduction Number, \( R_0 \) – It is defined as the average number of secondary infections caused by a single infected case in a fully susceptible population. Epidemic occurs when \( R_0 > 1 \) and fades out when \( R_0 < 1 \).
-
Effective Reproduction Number, \( R_{eff} \) – It is defined as the average number of secondary cases arising from an infected case, at a given point in an epidemic. At the start of the epidemic, \( R_{eff} > 1 \). If we need to stop transmission, then \( R_{eff} < 1 \)
-
Vectorial capacity – It is defined as the number of secondary cases arising per day from a single infective case in a totally susceptible human population.
-
Herd immunity – It is a situation where an infection cannot spread easily due to the number of immune people in a population. In mathematical terms, \( R_{eff} < 1 \). Herd immunity is raised artificially through the use of effective vaccination.
-
Deterministic model – A model that has only one possible output when all of its parameters are fully specified.
-
Stochastic model – A model that may produce a range of outputs despite having fully specified parameters, as a result of incorporating probabilistic processes.
The basic fundamental drivers of getting an epidemic disease is:
-
Rate of infection – how quickly or slowly a person is passing a disease.
-
Infectious Period – how long in duration will the person be remain infected by that disease.
Infectious Disease Modeling
The spread of infectious diseases can be unpredictable. In addition to this, modelling in real time has particular challenges, not least the speed at which data needs to be gathered and processed in order to inform models.
Infectious disease modeling is a great example of how an interdisciplinary approach to science can have significant impact on the world around us. Underpinning infectious disease modeling is mathematics. Through the use of differential equations and statistical techniques, we can project the outcome of different interventions scenarios and also study past epidemics. We can use mathematical models in different domains to get effective results. Mathematical modelling is increasingly being used to support public health decision-making in the control of infectious diseases.
Compartmental Models
It is a modelling approach where the population is divided into different compartments, representing their status of disease, demographics and other factors, and where mathematical equations are used to model transitions between different compartments.
In this approach, we divide the population into different compartments or divisions where we make a simple assumption that everyone in the same compartment is subjected to the same hazards.
Simple compartmental (I-R) Model
Imagine a cohort of people with an simple infectious disease. Assume that ultimately, everyone recovers from the infection after a certain infectious period. We can then organize a cohort into two compartments. One is the number of people still infected with the disease \( I \) and the other is the number of people who have recovered \( R \). We start with everyone in the infected compartment and end up with everyone in the recovered compartment as indicated in the below figure:
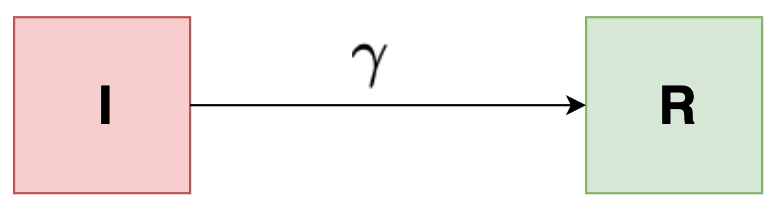
The basic question that could arise here is that how long does it take for people to move from one compartment to another? If we knew the infectious period, then could we predict how many people would be infected and recovered after one week, after a month, or how about after a year?
To model this, we’re going to introduce the rate of transition between I and R. We can model the dynamics of this cohort using just two differential equations:
\[\begin{align*} \frac{dI}{dt} &= -\gamma I \\ \frac{dR}{dt} &= \gamma I \end{align*}\]Here, \( \gamma \) is the recovery rate. This means that larger the value of \( \gamma \), more quickly will people go from \( I \) to \( R \).
Simple compartmental (I-M-R) Model
We can add the complexity to out previous model by introducing a new compartment \( M \) which indicates the mortality or number of people dying from the disease.
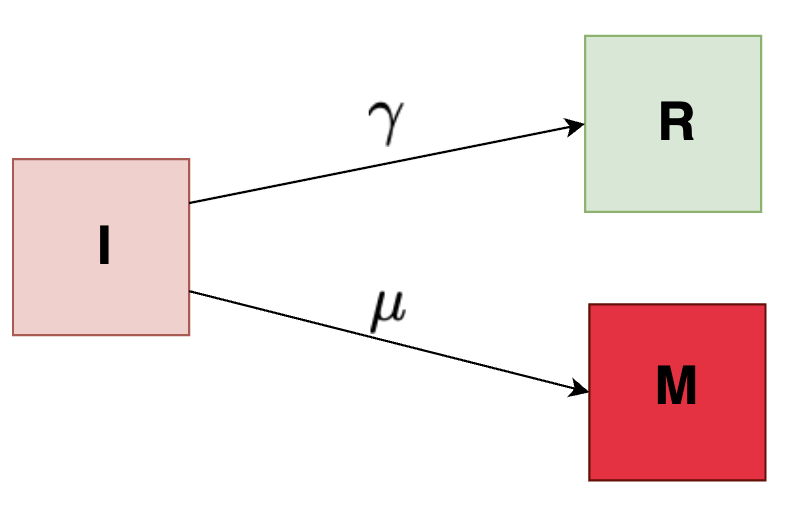
The required set of equations describing the functions are given below:
\[\begin{align*} I(t) &= 10^6 e^{-(\mu + \gamma)t} \\ M(t) &= 10^6 \frac{\mu}{\mu + \gamma}\left[1 - e^{-(\mu + \gamma)t} \right] \\ R(t) &= 10^6 \frac{\gamma}{\mu + \gamma}\left[1 - e^{-(\mu + \gamma)t} \right] \\ \end{align*}\]where, \( \gamma \) is the recovery rate and \( \mu \) is the mortality rate.
The correponding differential equations are given below:
\[\begin{align*} \frac{dI}{dt} &= -(\mu + \gamma) I \\ \frac{dM}{dt} &= \mu I \\ \frac{dR}{dt} &= \gamma I \end{align*}\]And then, we have some initial conditions, at time (t = 0):
\[\begin{align*} I &= 10^6 \\ M &= R = 0 \end{align*}\]When \(t = 0, M(t = 0) = 0 \) and when \(t > 0, M(t > 0) = 10^6 \frac{\mu}{\mu + \gamma} \)
SIR Model
This is one of the more frequently used compartmental-based infectious disease modeling. In the SIR model, the entire population is divided into three compartments: Incidence, \( S \); Prevalence, \( I \) and Recovery, \( R \).
Assumptions of this model are (i) homogeneous population – everyone in the same compartment is subject to the same hazards, (ii) well mixed population – All susceptible people have the same risk of getting infected for a given number of infected people.

For modeling force of infection, \( \lambda \), we need to consider that it changes over time. At the beginning of an epidemic there aren’t many infected people around, so the force of infection is very small. But as the epidemic starts to increase, more people move into the infectious compartment which drives up the force of infection. If we denote:
\[\begin{align*} p &= \text{per contact with an infectious person, probability of a susceptible person becoming infected} \\ c &= \text{Average number of contacts a susceptible make per day} \\ \frac{I}{N} &= \text{fraction of population that is infected} \end{align*}\]\[ \lambda = p c \frac{I}{N} = \beta \frac{I}{N} \]
Here, \( \beta \), also called infection term is not measured directly, but esimtated indirectly from data. The required differential equations for each state of this model is given as below:
\[\begin{align*} \frac{dS}{dt} &= -\beta S \frac{I}{N}\\ \frac{dI}{dt} &= \beta S\frac{I}{N} - \gamma I\\ \frac{dR}{dt} &= \gamma I \end{align*}\]\( \gamma, \beta \) = Model parameters while \( S, I, R \) = State of the system at a point in time.
\[ R_0 = \frac{\beta}{\gamma} \]
SEIR, SAIR, SEAIR Models
The previously discussed SIR model is one of the simplest compartmental models in infectious disease dynamics. It might be effective when we are assuming the situation where people are immediately infectious upon getting infected. However, in reality, we know that diseases can be more complex. Some infections involve an intermediate period when the pathogen is establishing itself within a host before individuals become infectious. Other infections involve an asymptomatic phase where individuals can pass on infection even without symptoms.
In order to account for the intermediate period of latent period, we can introduce a new state, \( E \) indicating latent phase, which suggests the number of people exposed implying having infection but are not yet infectious, and so we get the following figure:

In order to account for the asymptotic individuals, we introduce a new state \( A \) indicating compartment containting asymptotic individuals (carrying infections but has no symptoms) and so we get the following:

We can also add a different complexity to our model by adding compartments having incubation period for individuals in the population as shown in the following:
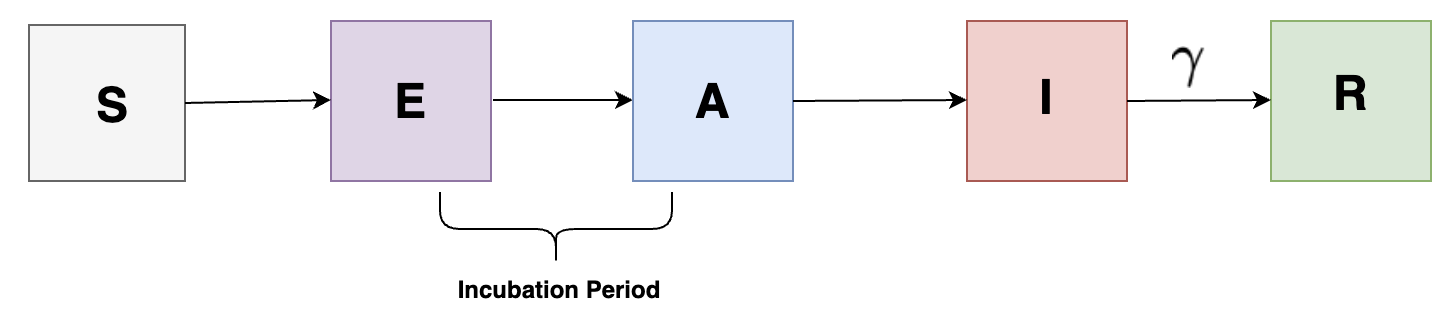
Interventions
The need to simulate the impact of different interventions on the disease transmission rate. Examples of interventions include – effect of vaccination in reducing susceptibility, effect of treatment on the recovery rate and so on.
Treatment or Vaccination
There is a use of mathematical models in looking at the potential impact of treatment or vaccination. Suppose, that we have a fully effective treatment that can cure people immediately and also we put people on treatment on average two days after their symptoms begin. In order to model this, we add an additional rate of transition from \( I \) to \( R \) to capture the effect of treatment.
If we consider the basic SIR model as seen earlier, then the model is appropriate for a disease where the population is relatively stable over time. So, we don’t need to worry about population turnover and where immunity doesn’t wane appreciably over the epidemic timescale.
\[\begin{align*} \frac{dS}{dt} &= -\beta S \frac{I}{N}\\ \frac{dI}{dt} &= \beta S\frac{I}{N}-(\gamma + h) I\\ \frac{dR}{dt} &= (\gamma + h) I \end{align*}\]How to counter the spread of disease?
Epidemic disease like flu, or in more recent times coronavirus has a large impact on causing infections at a rapid state since it transmits through contact. Now, looking at the big picture the question arises – How do we eliminate disease?. The most usual answer is – Through vaccination. But the other question comes – How do we provide vaccinations?. And this is where we need to think about in terms of social network world. Now, we can have some possible choices. If we have a network of people living in a region or a city and we go about vaccinating them randomly. Will it do the business of eliminating the disease? The answer would be a No!. Because the random people that are being provided the vaccines are not well-connected and therefore will not impact and reduction of the spread of the disease.
A major way to slow the spread of disease is to come with a strategy of tracing contacts that came in close contact with the infected person. This could be important since if we identify those close contacts then they can be monitor and notify with the necessary guidelines and recommendations. This can prove to be helpful in people to take preventive measures so that there is there is no further spread of disease. This is a key mechanism to limit the community spread.
Useful Resources
Paper – Modeling infectious disease dynamics in the complex landscape of global health
Paper – Factors that make an infectious disease outbreak controllable